Hình Đa Diện Nào Không Có Tâm Đối Xứng ?
Tiếp tục cùng Top10vietnam.net tìm hiểu các kiến thức liên quan đến hình đa diện và tìm câu trả lời cho câu hỏi hình đa diện nào không có tâm đối xứng nhé.
Tiếp tục cùng Top10vietnam.net tìm hiểu các kiến thức liên quan đến hình đa diện và tìm câu trả lời cho câu hỏi hình đa diện nào không có tâm đối xứng nhé.
Câu Hỏi: Hình Đa Diện Nào Không Có Tâm Đối Xứng ?
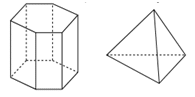
A. Lăng trụ lục giác đều
B. Tứ diện đều
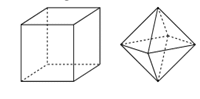
C. Lập phương
D. Bát điện đều
- Đáp án B – Tứ diện đều không có tâm đối xứng
+) Hình lăng trụ lục giác đều có tâm đối xứng là điểm I:
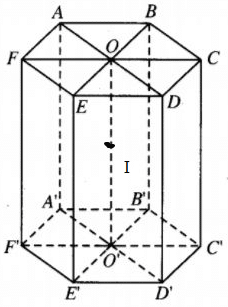
+) Hình tứ diện không có tâm đối xứng
+) Hình lập phương có tâm đối xứng là điểm O:
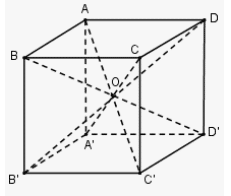
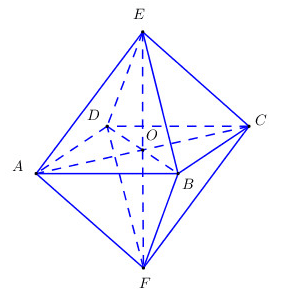
+) Hình bát diện đều có tâm đối xứng là điểm O:
Kiến thức liên quan: Hai Đa diện bằng nhau
Đối xứng tâm là gì?
– Định nghĩa: Điểm I gọi là tâm đối xứng qua hình H nếu điểm đối xứng với mỗi điểm thuộc hình H qua điểm I cũng thuộc hình H.
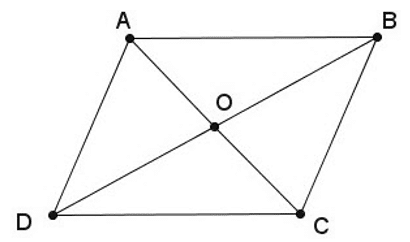
– Định lí: Giao điểm hai đường chéo của hình bình hành là tâm đối xứng của hình bình hành đó
Một số hình có tâm đối xứng
- Hình bình hành, tâm đối xứng của hình bình hành là giao điểm hai đường chéo.
- Đường tròn, tâm đối xứng của đường tròn là tâm của đường tròn.
- Hình chữ nhật, tâm đối xứng của hình chữ nhật là giao điểm hai đường chéo.
- Hình thoi, tâm đối xứng của hình thoi là giao điểm hai đường chéo.
- Hình vuông, tâm đối xứng của hình vuông là giao điểm hai đường chéo.
- Đa giác đều có số cạnh chẵn thì tâm đối xứng là giao điểm của các đường chéo nối liền 2 đỉnh đối diện nhau.
Phép dời hình trong không gian
• Trong không gian, quy tắc đặt tương ứng mỗi điểm M với điểm M’ xác định duy nhất được gọi là một phép biến hình trong không gian.
• Phép biến hình trong không gian được gọi là phép dời hình nếu nó bảo toàn khoảng cách giữa hai điểm tùy ý.
a) Phép tịnh tiến theo vectơ v→, là phép biến hình biến mỗi điểm M thành điểm M’ sao cho MM’→ = v→. Kí hiệu là Tv→ .
b) Phép đối xứng qua mặt phẳng (P) là phép biến hình biến mỗi điểm thuộc (P) thành chính nó, biến mỗi điểm M không thuộc (P) thành điểm M’ sao cho (P) là mặt phẳng trung trực của MM’.
Nếu phép đối xứng qua mặt phẳng (P) biến hình (H) thành chính nó thì (P) được gọi là mặt phẳng đối xứng của (H).
c) Phép đối xứng tâm O là phép biến hình biến điểm O thành chính nó, biến mỗi điểm M khác O thành điểm M’ sao cho O là trung điểm của MM’.
Nếu phép đối xứng tâm O biến hình (H) thành chính nó thì O được gọi là tâm đối xứng của (H).
d) Phép đối xứng qua đường thẳng Δ là là phép biến hình biến mọi điểm thuộc đường thẳng Δ thành chính nó, biến mỗi điểm M không thuộc Δ thành điểm M’ sao cho Δ là đường trung trực của MM’.
Nếu phép đối xứng qua đường thẳng Δ biến hình (H) thành chính nó thì Δ được gọi là trục đối xứng của (H).
Nhận xét:
• Thực hiện liên tiếp các phép dời hình sẽ được một phép dời hình.
• Phép dời hình biến đa diện (H) thành đa diện (H’), biến đỉnh, cạnh, mặt của (H) thành đỉnh, cạnh, mặt tương ứng của (H’).
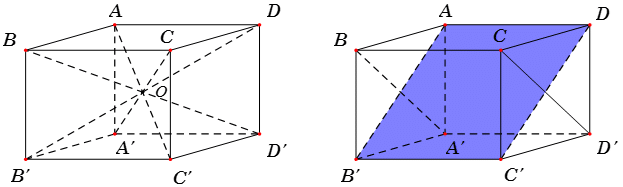
Ví dụ: Cho hình lập phương ABCD.A’B’C’D’. Khi đó:
– Các hình chóp A.A’B’C’D’ và C’.ABCD bằng nhau (vì qua phép đối xứng tâm O hình chóp A.A’B’C’D’ biến thành hình chóp C’.ABCD).
– Các hình lăng trụ ABC.A’B’C’ và AA’D’.BB’C’ bằng nhau (vì qua phép đối xứng qua mặt phẳng (AB’C’D) thì hình lăng trụ ABC.A’B’C’ biến thành hình lăng trụ AA’D’.BB’C’).
Phân chia và lắp ghép các khối đa diện
Nếu khối đa diện (H) là hợp của hai khối đa diện (H1) và (H2) sao cho (H1) và (H2) không có chung điểm trong nào thì ta nói có thể phân chia được khối đa diện (H) thành hai khối đa diện (H1) và (H2). Khi đó ta cũng nói có thể ghép hai khối đa diện (H1) và (H2) để được khối đa diện (H.
- Ví dụ: Với khối chóp tứ giác S.ABCD, xét hai khối chóp tam giác S.ABC và S.ACD. Ta thấy rằng:
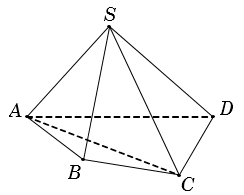
– Hai khối chóp S.ABC và S.ACD không có điểm trong chung (tức là không tồn tại điểm trong của khối chóp này là điểm trong của khối chóp kia và ngược lại).
– Hợp của hai khối chóp S.ABC và S.ACD chính là khối chóp S.ABCD
Vậy khối chóp S.ABCD được phân chia thành hai khối chóp S.ABC và S.ACD hay hai khối chóp S.ABC và S.ACD được ghép lại thành khối chóp S.ABCD
Hi vọng bài viết mà Top10vietnam.net chia sẻ trên đây đã cung cấp những kiến thức hữu ích giúp bạn đọc xác định được hình đa diện nào không có tâm đối xứng. Chúc bạn học tập tốt!



