Hình Đa Diện Có Bao Nhiêu Mặt
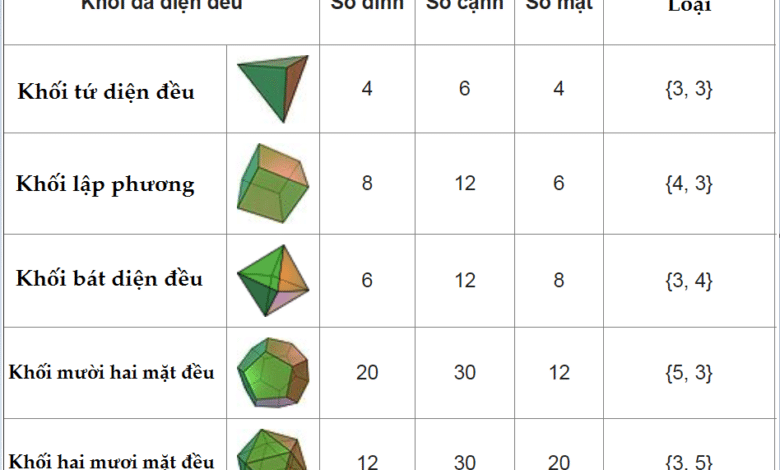
Hình đa diện là một hình rất quen thuộc xuất hiện trong chương trình Toán học lớp 12. Tuy nhiên để xác định được hình đa diện có bao nhiêu mặt đòi hỏi bạn cần năm vững các kiến thức cơ bản về loại hình học này. Cùng Top10vietnam.net tìm hiểu nội dung này qua bài viết dưới đây nhé!
Câu Hỏi: Hình đa diện có bao nhiêu mặt?
A. 9
B. 10
C. 11
D. 12
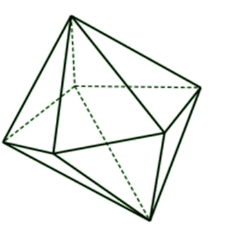
Đáp án: B – Hình Đa Diện có 10 mặt
Kiến thức liên quan
Cách xác định một mặt phẳng
- Qua ba điểm không thẳng hàng xác định một mặt phẳng duy nhất. Mặt phẳng đi qua ba điểm không thẳng hàng A, B, C được kí hiệu là mp(ABC) hay (ABC)
- Qua một đường thẳng và một điểm không thuộc đường thẳng đó xác định một mặt phẳng duy nhất. Mặt phẳng đi qua A và đường thẳng d không chứa A được kí hiệu là mp(A;d).
- Qua hai đường thẳng cắt nhau xác định một mặt phẳng duy nhất. Mặt phẳng qua hai đường thẳng cắt nhau a,b được kí hiệu là mp(a;b).
Các tính chất của hình học không gian
- Tính chất 1: Có một và chỉ một đường thẳng đi qua hai điểm phân biệt cho trước.
- Tính chất 2: Có một và chỉ một mặt phẳng đi qua ba điểm không thẳng hàng cho trước.
- Tính chất 3: Tồn tại bốn điểm không cùng nằm trên một mặt phẳng.
- Tính chất 4: Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng có một đường thẳng chung duy nhất chứa tất cả các điểm chung của hai mặt phẳng đó.
Hình Đa diện là gì?
Hình đa diện gồm hữu hạn các đa giác phẳng thỏa mãn hai điều kiện sau:
- Điều kiện 1: Với hai đa giác bất kỳ chỉ xảy ra một trong các trường hợp sau: Không có điểm chung; Có một đỉnh chung; Có 1 cạnh chung. Có nghĩa là hình có 2 đa giác mà không thuộc 3 trường hợp trên hoặc có nhiều hơn 1 trường hợp trong ba trường hợp trên đều không thỏa mãn.
Ví dụ:
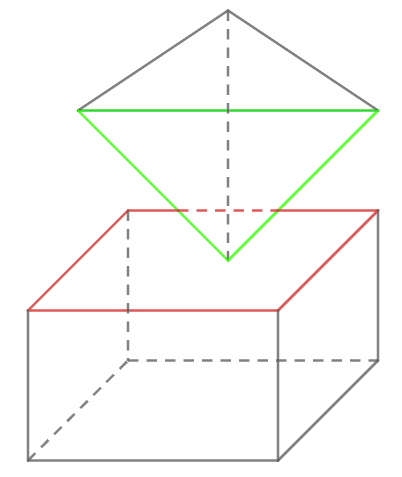
Hình trên không phải là hình biểu diễn của một hình đa dιện vì tam giác (màu xanh) và hình chữ nhật (màu đỏ) không thỏa mãn điều kiện 1. Cụ thể là 2 đa giác này có 1 điểm chung nhưng điểm chung đó lại không phải đỉnh chung.
- Điều kiện 2: Mỗi cạnh của một đa giác là cạnh chung của đúng hai đa giác. Nghĩa là có 1 cạnh của đa giác không là cạnh chung của 2 đa giác hoặc là cạnh chung của 3 đa giác trở lên đều vi phạm.
Ví dụ:
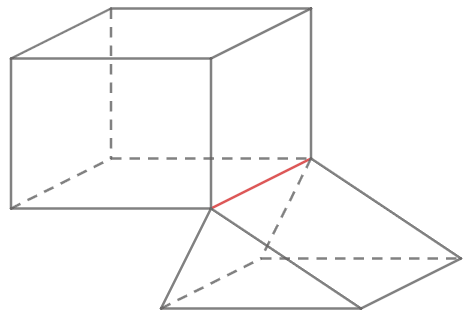
Hình trên không phải hình biểu diễn của hình đa dιện. Vì có 1 cạnh (màu đỏ) là cạnh chung của tới 4 mặt.
Các hình đa diện thường gặp mà chúng ta đã biết từ lớp 11 như: Hình tứ diện, hình chóp, hình lăng trụ, hình chóp cụt, hình hộp, hình lập phương…
Khối Đa Diện là gì?
Mỗi hình đa diện chia không gian thành miền trong và miền ngoài. Hình đa diện và miền trong của nó tạo thành khối đa diện. Hay nói cách khác mỗi hình đa diện có 1 khối đa diện tương tương ứng. Ví dụ khối tứ diện, khối chóp, khối lăng trụ, khối chóp cụt, khối hộp, khối lập phương… là các khối đa diện.
Khối đa diện được phân chia làm hai loại: Khối đa diện lồi và khối đa diện không lồi. Tuy nhiên trong chương trình THPT, chúng ta chỉ nghiên cứu khối đa diện lồi.
Khối đa diện lồi là khối đa diện mà đoạn thẳng nối 2 điểm bất kỳ thuộc khối đa diện thì nằm hoàn toàn trên khối đa diện đó.
Ví dụ: Khối chóp, khối lăng trụ là các khối đa diện lồi.
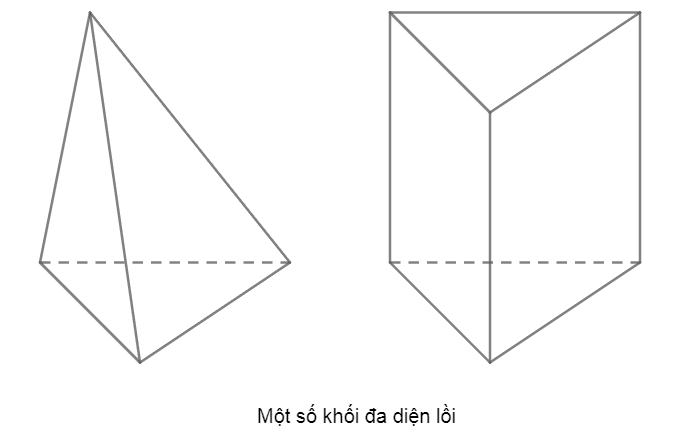
Ví dụ:
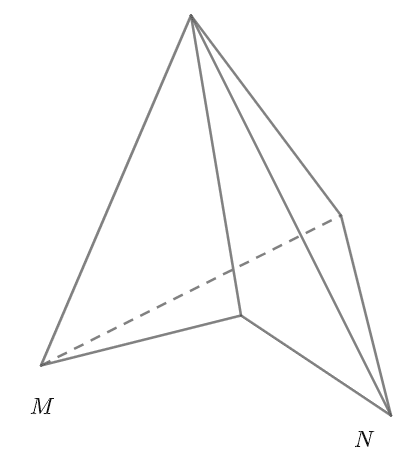
Hình trên không phải khối đa dιện lồi vì đoạn thẳng MN không nằm trên khối đa dιện.
Trên đây là tổng quan về hình đa diện và khối đa diện mà Top10vietnam.net giới thiệu đến các bạn. Hi vọng sau bài viết hình đa diện có bao nhiêu mặt, bạn đọc sẽ đón đọc thêm các bài viết tiếp theo để tìm hiểu nhiều kiên thức hơn. Chúc các bạn học tập tốt!


