Tam giác đều có tâm đối xứng không là sự băn khoăn của nhiều người. Hãy cùng Top10vietnam.net củng cố lại kiến thức về tam giác đều và tìm câu trả lời trong bài viết này nhé!
Câu hỏi: tam giác đều có tâm đối xứng không ?
Trả lời: Tam giác đều không có tâm đối xứng.
Kiến thức cần nhớ
1. Hai điểm đối xứng qua một điểm
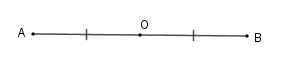
Định nghĩa: Hai điểm AA, BB gọi là đối xứng với nhau qua điểm OO nếu OO là trung điểm của đoạn thẳng nối hai điểm đó.
Quy ước: Điểm đối xứng với điểm OO qua điểm OO cũng là điểm OO
Ví dụ: BB đối xứng với AA qua OO nếu OO là trung điểm của ABAB
2. Hai hình đối xứng qua một điểm
Định nghĩa: Hai hình gọi là đối xứng với nhau qua điểm OO nếu mỗi điểm thuộc hình này đối xứng với mỗi điểm thuộc hình kia qua điểm OO và ngược lại. Điểm OO gọi là tâm đối xứng của hai hình đó.
Chú ý: Nếu hai đoạn thẳng (góc, tam giác) đối xứng với nhau qua một điểm thì chúng bằng nhau.
3. Hình có tâm đối xứng
Định nghĩa: Điểm OO gọi là tâm đối xứng của hình HH nếu điểm đối xứng với mỗi điểm thuộc hình HH qua điểm OO cũng thuộc hình HH . Ta nói hình HH có tâm đối xứng.
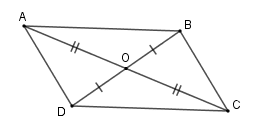
Định lý: Giao điểm hai đường chéo của hình bình hành là tâm đối xứng của hình bình hành đó.
Ví dụ: Giao điểm OO của ACAC và BDBD là tâm của hình bình hành ABCD.ABCD.
4. Định nghĩa về tam giác đều
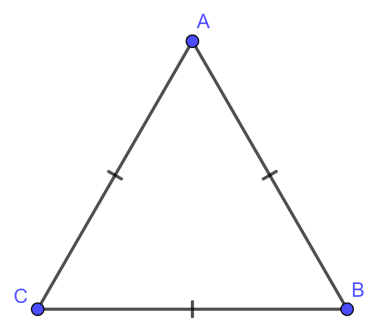
Trong hình học, tam giác đều là tam giác có ba cạnh bằng nhau hoặc tương đương ba góc bằng nhau và bằng 60°. Nó là một đa giác đều với số cạnh bằng 3.
Trong tam giác ABC đều có AB = AC = BC.
Hệ quả:
- Trong một tam giác đều thì mỗi góc bằng 60°
- Nếu một tam giác có 3 góc bằng nhau thì đó là tam giác đều.
- Nếu một tam giác cân có 1 góc bằng 60° thì đó là tam giác đều.
5. Tính chất của tam giác đều
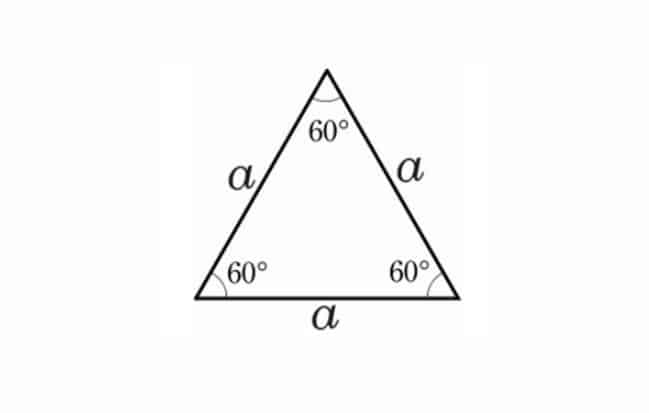
Trong tam giác đều gồm có 5 tính chất, đó là:
- Trong một tam giác đều, mỗi góc bằng 600. (Tam giác ABC đều ∠A = ∠B = ∠C = 600.)
- Nếu một tam giác có ba góc bằng nhau thì tam giác đó là tam giác đều. ( ∠A = ∠B = ∠C thì là tam giác ABC đều.)
- Nếu một tam giác cân có một góc bằng 600 thì tam giác đó là tam giác đều.
- Trong tam giác đều, đường trung tuyến của tam giác đồng thời là đường cao và đường phân giác của tam giác đó.
- Tam giác ABC đều có AD là đường trung tuyến kẻ từ đỉnh A. Khi đó, AD là đường cao và đường phân giác của tam giác ABC.
6. Các dạng toán thường gặp
Dạng 1: Tính độ dài cạnh, chu vi tam giác, tứ giác.
- Phương pháp:
Sử dụng chú ý: Nếu hai đoạn thẳng (góc, tam giác) đối xứng với nhau qua một điểm thì chúng bằng nhau.
Dạng 2: Xác định tâm đối xứng của một hình. Xác định các yếu tố đối xứng nhau qua một điểm. Chứng minh các hệ thức hình học.
- Phương pháp:
Ta thường sử dụng các định nghĩa và định lý sau:
+ Hai điểm A, B gọi là đối xứng với nhau qua điểm O nếu O là trung điểm của đoạn thẳng nối hai điểm đó.
+ Giao điểm hai đường chéo của hình bình hành là tâm đối xứng của hình bình hành đó.
Hình có tâm đối xứng
Những hình có một điểm O sao cho khi quay nửa vòng quanh điểm O ta được vị trí mới của hình chồng khít với vị trí ban đầu (trước khi quay) thì được gọi là hình có tâm đối xứng và điểm O được gọi là tâm đối xứng của hình.
- Ví dụ:
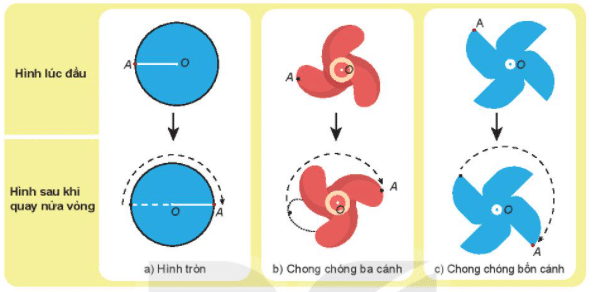
+ Các hình tròn và chong chóng bốn cánh dưới đây là các hình có tâm đối xứng vì khi quay nửa vòng quanh điểm O thì hình thu được chồng khít với chính nó ở vị trí ban đầu.
+ Ta thấy hình chong chóng ba cánh khi quay nửa vòng quanh điểm O thì hình thu được không chồng khít với chính nó ở vị trí ban đầu => Hình này không có tâm đối xứng.
Tâm đối xứng của một số hình
- Tâm đối xứng của hình bình hành, hình thoi, hình vuông, hình chữ nhật là giao điểm của hai đường chéo.
- Tâm đối xứng của hình lục giác đều là giao điểm của các đường chéo chính.
Lưu ý:
- Có những hình có tâm đối xứng và có nhiều trục đối xứng: Hình tròn, hình vuông, hình chữ nhật, hình thoi.
- Có hình không có tâm đối xứng: Tam giác đều, hình thang cân,..
Như vậy trên đây chúng ta đã cùng nhau ôn lại các kiến thức về tam giác đều. Bao gồm lý thuyết về đối xứng tâm, định nghĩa, các tính chất, dấu hiệu nhận biết và công thức của tam giác đều rồi.
Top10vietnam.net hi vọng với những kiến thức bổ ích này sẽ giúp các bạn trả lời được câu hỏi tam giác đều có tâm đối xứng không, qua đó ôn tập và rèn luyện lại kiến thức về tam giác đều của mình một cách tốt nhất.
