Hình Bình Hành Có Mấy Trục Đối Xứng ?
Hình bình hành chắc hẳn rất quen thuộc với nhiều người, tuy nhiên đa số chưa nắm hết được toàn bộ kiến thức xoay quanh hình bình hành. Sau đây, Top10vietnam.net sẽ tổng hợp kiến thức về hình này và giúp bạn trả lời câu hỏi hình bình hành có mấy trục đối xứng ? hình bình hành có trục đối xứng không ?
Hình bình hành chắc hẳn rất quen thuộc với nhiều người, tuy nhiên đa số chưa nắm hết được toàn bộ kiến thức xoay quanh hình bình hành. Sau đây, Top10vietnam.net sẽ tổng hợp kiến thức về hình này và giúp bạn trả lời câu hỏi hình bình hành có mấy trục đối xứng ? hình bình hành có trục đối xứng không ?
Câu hỏi: Hình Bình Hành Có Mấy Trục Đối Xứng Hình Bình Hành Có Trục Đối Xứng Không
Hình bình hành có trục đối xứng không?
- Có
- Không
Đáp án chính xác là đáp án A . Hình Bình Hành Có Trục Đối Xứng.
Hình bình hành có mấy trục đối xứng?
A. 1.
B. 2.
C. 4.
D. 0.
Đáp án chính xác là đáp án D. Hình bình hành không có trục đối xứng.
Kiến thức liên quan
Phương pháp xác định trục đối xứng
Sử dụng định nghĩa của phép đối xứng trục.
a) Hai điểm gọi là đối xứng với nhau qua đường thẳng d nếu d là đường trung trực của đoạn thẳng nối hai điểm đó.
Quy ước: Nếu B∈d thì ta nói B đối xứng với B qua d.
b) Hai hình gọi là đối xứng với nhau qua đường thẳng d nếu mỗi điểm thuộc hình này đối xứng với một điểm thuộc hình kia qua đường thẳng d và ngược lại. Đường thẳng d gọi là trục đối xứng của hai hình đó.
Trục đối xứng của một số hình
a) Đường trung trực của một đoạn thẳng là trục đối xứng của đoạn thẳng đó.
b) Tia phân giác của một góc là trục đối xứng của góc đó.
c) Đường trung trực của cạnh đáy tam giác cân là trục đối xứng của tam giác cân đó.
d) Đường trung trực của các cạnh tam giác đều là các trục đối xứng của tam giác đều đó. e) Đường thẳng đi qua trung điểm hai đáy của hình thang cân là trục đối xứng của hình thang cân đó.
f) Mỗi đường kính của hình tròn là một trục đối xứng của hình tròn đó
Định nghĩa hình bình hành
Hình bình hành là tứ giác có các cạnh đối song song
Ví dụ: Ta có AB // CD, AD // BC thì ABCD là hình bình hành.
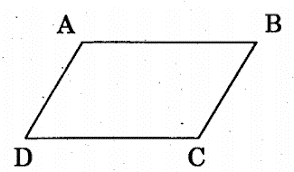
Nhận xét: Hình bình hành là hình thang có hai cạnh bên song song.
Tính chất hình bình hành
- Các cạnh đối HBH bằng nhau.
- Các góc đối HBH bằng nhau.
- Hai đường chéo hình bình hành cắt nhau tại trung điểm mỗi đường.
Dấu hiệu nhận biết
Hình bình hành là tứ giác đặc biệt:
- Tứ giác có các cạnh đối song song. (g.c.g)
- Tứ giác có các cạnh đối bằng nhau. (c.c.c).
- Tứ giác có hai cạnh đối song song và bằng nhau. (c.g.c)
- Tứ giác có các góc đối bằng nhau. (g.g.g hoặc g.c.g)
- Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường.
Chú ý: Hình bình hành là một hình thang đặc biệt (hình bình hành là hình thang có hai cạnh bên song song).
Quy tắc hình bình hành
Quy tắc: Tổng hai vectơ cạnh chung điểm đầu một HBH bằng vectơ đường chéo có cùng điểm đầu đó.
Ví dụ: Cho HBH ABCD, có →AB+ →AD= →AC.
Chứng minh: Dựa vào hai vectơ bằng nhau và quy tắc 3 điểm.
- Trả lời:
Vì →AD=→BC nên →AB+→AD=→AB+→BC=→AC.
Trên đây là toàn bộ kiến thức tổng quát liên quan hình bình hành, Top10vietnam.net rất mong đem đến thông tin bổ ích tới độc giả, qua đó giúp bạn có câu trả lời cho câu hỏi hình bình hành có mấy trục đối xứng ? hình bình hành có trục đối xứng không ?



